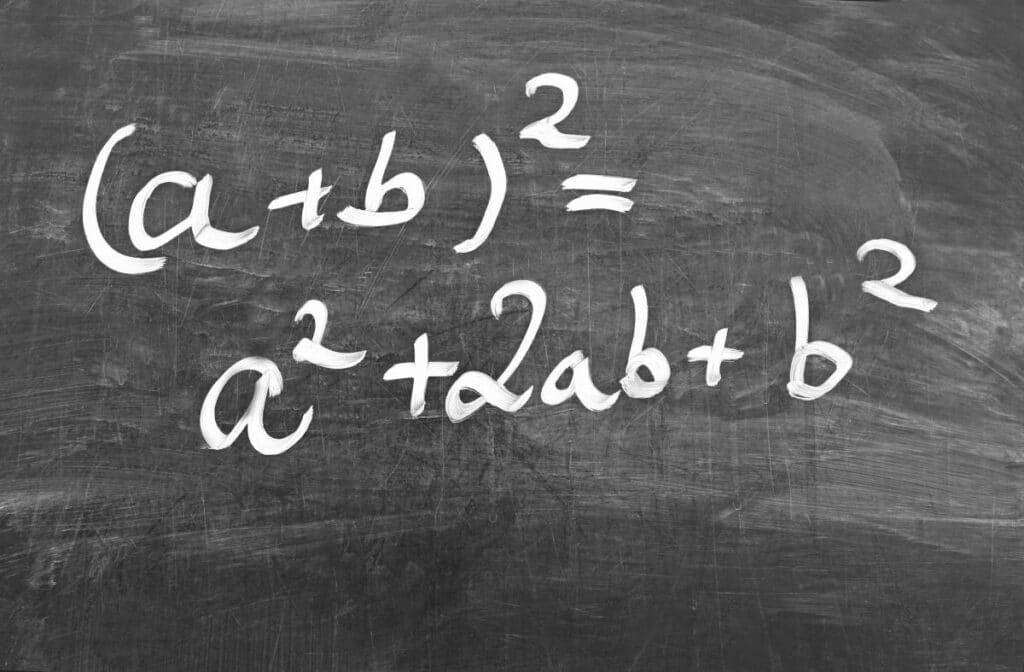Das Wichtigste in Kürze
Was genau sind binomische Formeln?
Binomische Formeln sind mathematische Formeln, die in der algebraischen Mathematik verwendet werden, um die Potenzen einer Summe von zwei Ausdrücken zu berechnen. Sie sind auch als binomische Theorem oder Newton-Leibniz Formel bekannt.
Wie viele verschiedene binomische Formeln gibt es?
Es gibt 3 binomische Formeln.
Wie berechnet man binomische Formeln?
Die binomischen Koeffizienten (n über k) sind die Koeffizienten vor jedem Summanden und berechnet sich als n! / (k! * (n-k)!) . Wenn man die binomische Formel anwendet, sollte man das n (die Potenz) und die binomischen Koeffizienten kennen und die Potenzen von a und b berechnen können und die Summe bilden.
Binomische Formeln sind eine wichtige Grundlage in der Mathematik. Doch gerade wenn Du die Formeln erst neu lernst, sind sie nicht ganz einfach zu verstehen. Um Dir zu helfen, die Formeln richtig anzuwenden, haben wir Dir hier alles Wissenswerte zusammengefasst.
Du erfährst alles darüber, wie man binomische Formeln berechnet und wie man Binome auflöst.

Inhalt
Entdecke die Macht der binomischen Formeln
Du hast bestimmt schon einmal von der binomischen Formel gehört, aber hast Du jemals darüber nachgedacht, wie nützlich sie sein kann? Die binomische Formel ermöglicht es uns, binomische Ausdrücke schnell und einfach aufzulösen, ohne mühsam jeden einzelnen Term berechnen zu müssen.
Zunächst einmal, was ist ein binomischer Ausdruck? Ein binomischer Ausdruck ist ein Ausdruck, der aus zwei Termen besteht, die durch ein Plus- oder Minuszeichen getrennt sind. Beispiele für binomische Ausdrücke sind (a + b) oder (a – b). In der binomischen Formel wird ein binomischer Ausdruck mit (x + y)^n dargestellt, wobei n der Exponent des Ausdrucks ist.
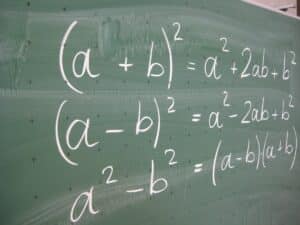
Binomische Formeln sind mathematische Formeln, die aus zwei Termen bestehen. Diese Terme können Zahlen, Variablen oder mathematische Ausdrücke sein. Die Binomische Formel gibt an, wie Du aus den beiden Termen einen Ausdruck berechnen kannst.
Die bekannteste Binomische Formel ist die Plus-Minus-Formel. Sie besagt, dass Du aus den beiden Termen einer Binomischen Formel eine Summe und eine Differenz berechnen kannst.
Die drei binomischen Formeln sind:
1. binomische Formel: (a + b)^2 = a^2 + 2ab + b^2
2. binomische Formel: (a – b)^2 = a^2 – 2ab + b^2
3. binomische Formel: (a + b)(a – b) = a^2 – b^2.
Diese Formeln werden verwendet, um bestimmte Ausdrücke zu vereinfachen oder zu expandieren. Sie sind besonders nützlich in der Algebra und in der Mathematik im Allgemeinen.

Die 1. binomische Formel
Die erste binomische Formel ist (a + b)^2 = a^2 + 2ab + b^2.
Diese Formel besagt, dass man das Quadrat einer Summe von zwei Zahlen auf eine andere Art schreiben kann. Um dies zu verstehen, denke daran, dass a^2 das Quadrat von a und b^2 das Quadrat von b ist.
Wenn wir a und b addieren, erhalten wir das Quadrat von a + b. Aber warum ist da noch 2ab dabei? Das liegt daran, dass ab die Multiplikation von a und b ist. Daher haben wir a^2, das Quadrat von a, 2ab, die Multiplikation von a und b, und b^2, das Quadrat von b.
Die 2. binomische Formel
Die zweite binomische Formel lautet (a – b)^2 = a^2 – 2ab + b^2.
Diese Formel ist sehr ähnlich zur ersten Formel, aber statt einer Addition haben wir hier eine Subtraktion. Um es zu verstehen, denke daran, dass (a – b) das Ergebnis der Subtraktion von a und b ist.
Wenn wir das Quadrat dieses Ergebnisses berechnen, erhalten wir a^2 – 2ab + b^2.
Die 3. binomische Formel
Die dritte binomische Formel ist (a + b)(a – b) = a^2 – b^2.
Diese Formel besagt, dass das Produkt einer Summe und einer Differenz gleich dem Unterschied der beiden Quadrate ist.
Hier haben wir a + b, die Summe von a und b, und a – b, die Differenz von a und b. Wenn wir sie multiplizieren, erhalten wir a^2 – b^2.
Binome auflösen – So gehst Du vor
Wenn Du ein Binom auflösen möchtest, musst Du zunächst die binomische Formel kennen. Anschließend kannst Du das Binom einfach nach der Plus-Minus-Formel ausrechnen. Diese besagt, dass jedes Binom (a + b)^n sich in n binomische Zahlen aufteilt.
Ein Beispiel: Du möchtest (x + y)^2 auflösen. Hierbei handelt es sich um ein Quadrat, das Du mit der Plus-Minus-Formel aufrechnen kannst. Das Ergebnis lautet x^2 + 2xy + y^2.
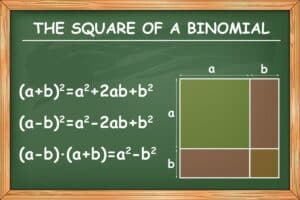
Beispiel der 1. binomischen Formel
Mit realen Zahlen lässt es sich besser verstehen. Hier ist ein Beispiel:
(2 + 3)^2 = (2 + 3) * (2 + 3)
Um diese Formel zu berechnen, musst Du zunächst die beiden Klammern ausrechnen:
(2 + 3) = 5
Jetzt kannst Du die Formel weiter berechnen:
(5)^2 = 5 * 5
= 25
Das Ergebnis lautet also 25.
Mit der binomischen Formel (a + b)^2 berechnest Du also das Quadrat einer Summe aus zwei Zahlen a und b. Wichtig ist hierbei, dass Du die beiden Klammern erst ausrechnest, bevor Du das Quadrat berechnest.
Binomische Formeln rechnen – Tipps und Tricks
Wenn Du binomische Formeln rechnen möchtest, gibt es ein paar Tipps und Tricks, die Dir dabei helfen können. Hier sind einige davon:
- Übe regelmäßig: Je mehr Du übst, desto besser wirst Du im Rechnen mit binomischen Formeln.
- Verwende Karteikarten: Schreibe die Formeln auf Karteikarten und übe immer wieder, bis Du sie auswendig kennst.
- Benutze eine Formeltabelle: Es gibt viele Formeltabellen im Internet, die Du kostenlos herunterladen und ausdrucken kannst.
- Hol Dir Hilfe von einem Mathematiklehrer: Wenn Du Probleme hast, kannst Du Dich an Deinen Mathematiklehrer wenden. Dieser kann Dir Tipps und Tricks geben, wie Du besser mit binomischen Formeln rechnen kannst.
Binomische Summen und Differenzen
Ein weiteres Anwendungsgebiet der binomischen Formel ist die Berechnung von binomischen Summen und Differenzen. Diese können verwendet werden, um die Summe oder den Unterschied zweier binomischer Ausdrücke zu berechnen, ohne jeden einzelnen Term ausrechnen zu müssen. Beispiele für binomische Summen und Differenzen sind (a + b)^2 – (a – b)^2 oder (a + b)(a – b).
In der Mathematik und in anderen Wissenschaftsdisziplinen finden sich oft binomische Ausdrücke und die binomische Formel ist ein wertvolles Werkzeug, um diese schnell und einfach aufzulösen. Es ist wichtig, die binomische Formel zu verstehen und zu wissen, wie man sie anwendet, um Probleme in der Mathematik, Physik, Ingenieurwissenschaft und Finanzmathematik zu lösen.
Es gibt auch viele Online-Ressourcen und Tools, die Dir helfen können, binomische Formeln zu rechnen und binomische Ausdrücke aufzulösen. Es lohnt sich auch, sich mit der Plus-Minus-Formel auseinandersetzen, da diese eng mit der binomischen Formel verwandt ist und ebenfalls hilfreich sein kann, binomische Ausdrücke aufzulösen.
Binomische Formeln in der Praxis
Die binomischen Formeln können genutzt werden, um Ausdrücke zu vereinfachen und zu expandieren.
Eines der Hauptanwendungsgebiete der binomischen Formeln ist die Algebra. Hier kannst Du sie verwenden, um schwierige Ausdrücke zu vereinfachen, bevor Du weiterrechnest. Auch in der Geometrie kannst Du die binomischen Formeln verwenden.
Tipp: Um die Anwendung der binomischen Formeln zu erleichtern, kannst Du Dir eine Tabelle oder eine Übersicht erstellen, die die binomischen Koeffizienten für verschiedene Werte von n enthält. Dies kann dabei helfen, schnell die richtigen Koeffizienten zu finden und die Potenzen von a und b schneller berechnen zu können.

Wie man binomische Formeln mit dem Taschenrechner löst
Du hast eine binomische Formel und möchtest sie mit dem Taschenrechner lösen? Kein Problem! Hier ist eine Anleitung, wie Du das Schritt für Schritt machen kannst.
- Stelle sicher, dass Dein Taschenrechner die Funktion (a + b)^n unterstützt. Das ist die binomische Formel in der kompakten Schreibweise.
- Gib die Werte für a und b ein. In der binomischen Formel steht (a + b)^n, deshalb musst Du zuerst a und b eingeben.
- Gib den Wert für n ein. n steht für die Potenz, die (a + b) erhält.
- Drücke die Potenz-Taste (^) auf Deinem Taschenrechner.
- Du solltest nun eine Ausgabe erhalten, die die binomische Formel in ausgeklügelter Schreibweise darstellt.
- Wenn Du die einzelnen Terme der binomischen Formel berechnen möchtest, musst Du die Kombinatorik-Funktion (n über k) verwenden. Diese Funktion berechnet die Anzahl der Möglichkeiten, k Elemente aus einer Menge von n Elementen auszuwählen.
- Drücke die Kombinatorik-Taste (nCr oder nCk) auf Deinem Taschenrechner und gib die Werte für n und k ein.
- Du solltest jetzt die einzelnen Terme der binomischen Formel erhalten.
Hinweis: Es gibt ein paar Taschenrechner, die die binomischen Formeln nicht unterstützt, in diesem Fall kannst Du die binomische Formel auch manuell berechnen.

Mit binomischen Formeln rechnen
Die binomische Formel ist ein mathematisches Werkzeug, das es ermöglicht, Potenzen von binomischen Ausdrücken (Ausdrücke mit a + b und a – b) auf einfachere Ausdrücke zu reduzieren.
Es gibt zwei Versionen der binomischen Formel: die erste ist für (a+b)^n, die zweite für (a-b)^n. Diese Formeln erlauben es, jeden Summanden einer Potenz von (a+b) oder (a-b) auszudrücken, indem die binomischen Koeffizienten verwendet werden.
Diese Koeffizienten sind die Koeffizienten vor jedem Summanden und berechnen sich als n! / (k! * (n-k)!). Um die binomische Formel anwenden zu können, sollte man das n (die Potenz) und die binomischen Koeffizienten kennen und die Potenzen von a und b berechnen können.
Das Rechnen mit binomischen Formeln kann, wie Du siehst, ganz einfach sein!
FAQ: Binomische Formel
Woran kann ich binomische Formeln erkennen?
Man kann binomische Formeln durch die binomischen Koeffizienten erkennen, die sich als n! / (k! * (n-k)!) berechnen und vor jedem Summanden in der Formel stehen.
Woher stammt der Name binomische Formeln?
Der Name „binomische Formel“ kommt von dem lateinischen Wort „binomium“, was „zwei Namen“ bedeutet. Dieser Name spiegelt die Tatsache wider, dass die Formel verwendet wird, um Potenzen von Ausdrücken der Form (a + b) oder (a – b) zu berechnen, die „zwei Namen“ enthalten.
Wie sehen die drei binomischen Formeln aus?
- Die erste binomische Formel: (a + b)^2 = a^2 + 2ab + b^2
- Die zweite binomische Formel: (a + b)^2 = a^2 – 2ab + b^2
- Die dritte binomische Formel: (a + b)(a – b) = a^2 – b^2.