Das Wichtigste in Kürze
Der Logarithmus ist ein mathematischer Weg, um exponentielle Berechnungen auf einem linearen Niveau durchzuführen. Er ist nützlich, wenn es darum geht, eine Potenz eines numerischen Wertes zu bestimmen.
Es gibt insgesamt fünf Logarithmusgesetze, allerdings gibt es neben der Gesetze auch eine Vielzahl an verschiedenen praktischen Tipps, die angewendet werden können. Erfahre hier Tipps zum Rechnen mit Logarithmus…
Die wichtigsten drei Logarithmusgesetze sind das Produktgesetz, das Quotientengesetz und das Potenzgesetz. Mehr Informationen zu den einzelnen Logarithmusgesetzen erfährst Du hier…
Log Regeln sind ein wichtiger Bestandteil der Mathematik und haben Anwendungen in vielen Bereichen wie Wissenschaft, Technik und Finanzen. Obwohl der Begriff für einige einschüchternd sein kann, ist das Konzept der Logarithmen relativ einfach zu verstehen und kann bei der Lösung von komplexen mathematischen Problemen hilfreich sein. In diesem Artikel erfährst Du alles über die Grundlagen der Logarithmen, wie Du mit Logarithmen addieren kannst und ihn richtig anwendest.
Inhalt
Logarithmus – Was ist das eigentlich?

Ein Logarithmus ist eine Funktion, die die Beziehung zwischen einer Basis und einer Potenz ausdrückt. Anders ausgedrückt, ein Logarithmus ist eine Potenzfunktion, die angewendet wird, um die Potenz einer Zahl zu bestimmen, die man benötigt, um eine andere Zahl zu erhalten. Logarithmen sind das Gegenteil von Exponenten, und sie werden oft als Log bezeichnet.
Der einfachste Weg, den Logarithmus zu verstehen, besteht darin, sich vorzustellen, dass er eine Art „Rechentrick“ ist, mit dem man schwierige Berechnungen vereinfachen kann. Zum Beispiel kann der Logarithmus verwendet werden, um zu berechnen, wie oft eine Zahl mit sich selbst multipliziert werden muss, um eine andere Zahl zu erhalten. Eine wichtige Eigenschaft von Logarithmen ist, dass sie die Multiplikation von Zahlen in das Addieren von Logarithmen umwandeln können, was insbesondere bei der Berechnung von sehr großen oder sehr kleinen Zahlen nützlich ist.
Die Logarithmus Formel lautet:
log_b(x) = yLogarithmen werden in der Regel in Bezug auf eine bestimmte Basis ausgedrückt, die normalerweise eine Zahl zwischen 2 und 10 ist. Die am häufigsten verwendeten Basen sind 10 und e (die Eulersche Zahl, ca. 2,718). Der Logarithmus wird in der Regel als „log“ gefolgt von der Basis und dem Argument (also der Zahl, von der man den Logarithmus berechnen möchte) geschrieben.
Die Eulersche Zahl: Die Eulersche Zahl ist eine irrationale Zahl, die unendlich viele Nachkommastellen hat, ohne ein sich wiederholendes Muster zu bilden. Bis heute wurden mehr als 22 Billionen Stellen von e berechnet, und es wird davon ausgegangen, dass es unendlich viele weitere Stellen gibt, die noch nicht berechnet wurden.
Warum Logarithmen so wichtig sind

Logarithmen sind eine wichtige mathematische Funktion, die in vielen Bereichen der Mathematik, Wissenschaft und Technik Anwendung finden. Im Folgenden werden wir uns damit beschäftigen, warum Logarithmen so wichtig sind.
- Vereinfachung von Berechnungen: Indem Logarithmen die Multiplikation von Zahlen in das Addieren der jeweiligen Logarithmen umwandeln, können Logarithmen die Berechnung von Produkten und Quotienten erheblich vereinfachen.
- Analyse von Daten und Algorithmen: Indem sie die Anzahl der Schritte, die ein Algorithmus benötigt, um eine bestimmte Aufgabe zu erledigen, in eine Funktion umwandeln, können Logarithmen helfen, die Effizienz von Algorithmen zu analysieren.
- Finanzmathematik und Statistik: Logarithmen ermöglichen es, komplexe Finanzinstrumente zu bewerten und zu vergleichen, indem sie die zeitliche Veränderung von Zinssätzen und Kursen berücksichtigen.
- Naturwissenschaften und Ingenieurwesen: In der Physik werden Logarithmen oft zur Beschreibung von Größen wie Schalldruckpegel, Lichtintensität und radioaktiver Zerfallsrate verwendet. Logarithmen ermöglichen es, große Zahlenbereiche zu komprimieren und Messungen in einer leichter verständlichen Form darzustellen.
Die wichtigsten Logarithmus Rechenregeln
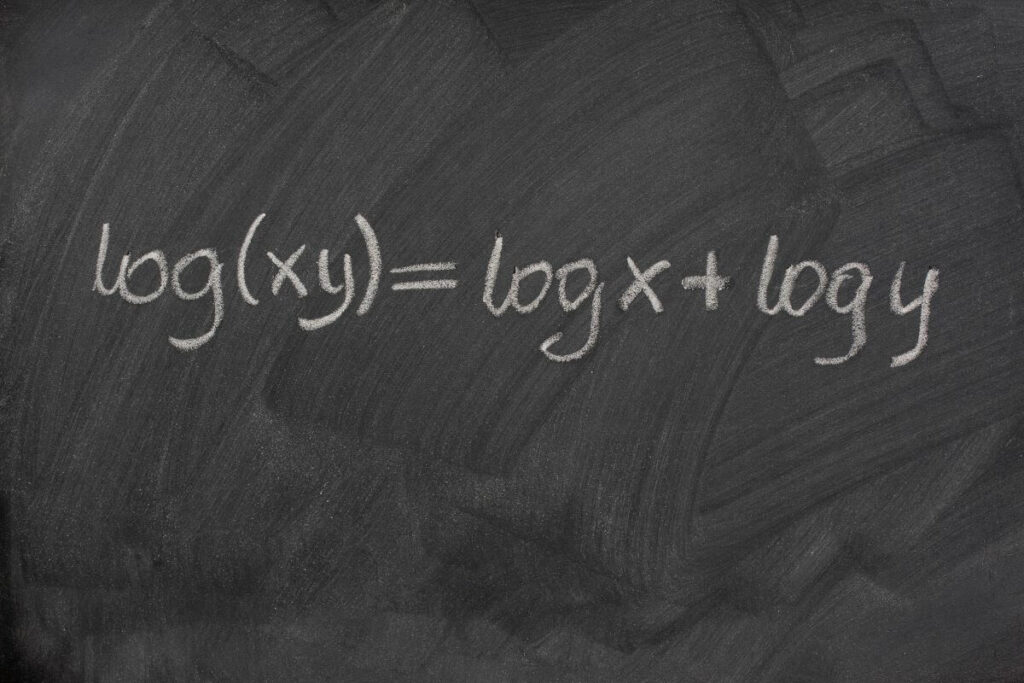
Logarithmen sind eine wichtige mathematische Funktion, die in vielen Bereichen Anwendung finden. Sie werden in der Regel in Bezug auf eine bestimmte Basis ausgedrückt, die normalerweise eine Zahl zwischen 2 und 10 ist. Die am häufigsten verwendeten Basen sind 10 und e (die Eulersche Zahl: 2,718). In diesem Artikel werden wir uns mit den wichtigsten Rechenregeln für Logarithmen beschäftigen, um Dir zu helfen, komplexe Berechnungen durchzuführen.
Multiplikationsregel
Die Multiplikationsregel ist eine Log Regel, die besagt, dass der Logarithmus des Produkts von zwei Zahlen gleich der Summe der Logarithmen der einzelnen Zahlen ist. Anders ausgedrückt, der Logarithmus eines Produkts ist gleich der Summe der Logarithmen der Faktoren.
Formel für die Multiplikationsregel:
log_b(x*y) = log_b(x) + log_b(y)Beispiel: Der Logarithmus von 10*100 zur Basis 10 ist:
log_10(10*100) = log_10(10) + log_10(100)
log_10(1000) = 1 + 2
log_10(1000) = 3Das bedeutet, 10*100 = 1000, oder anders ausgedrückt, 10^1 * 10^2 = 10^3.
Divisionsregel
Die Divisionsregel besagt, dass der Logarithmus des Quotienten von zwei Zahlen gleich der Differenz der Logarithmen der einzelnen Zahlen ist. Anders ausgedrückt, der Logarithmus eines Quotienten ist gleich der Differenz der Logarithmen des Zählers und des Nenners.
Formel für die Divisionsregel:
log_b(x/y) = log_b(x) - log_b(y)Beispiel: Der Logarithmus von 100/10 zur Basis 10 ist:
log_10(100/10) = log_10(100) - log_10(10)
log_10(10) = 2 - 1
log_10(10) = 1Das bedeutet, 100/10 = 10, oder anders ausgedrückt, 10^2 / 10^1 = 10^1.
Potenzregel
Die Potenzregel ist eine Log Regel, die besagt, dass der Logarithmus einer Potenz aus einer Zahl gleich dem Produkt des Exponenten und dem Logarithmus der Basis ist. Anders ausgedrückt, der Logarithmus einer Potenz ist gleich dem Exponenten mal dem Logarithmus der Basis.
Formel für die Potenzregel:
log_b(x^n) = n * log_b(x)Beispiel: Der Logarithmus von 10^3 zur Basis 10 ist:
log_10(10^3) = 3 * log_10(10)
log_10(1000) = 3 * 1
log_10(1000) = 3Das bedeutet, 10^3 ergibt gleich 1000.
Umkehrregel
Die Umkehrregel besagt, dass der Logarithmus einer Zahl gleich dem Exponenten der Basis ist. Anders ausgedrückt, wenn wir den Logarithmus einer Zahl kennen und die Basis kennen, können wir den Exponenten berechnen.
Formel für die Umkehrregel:
log_b(x) = y ==> b^y = xBeispiel: Der Logarithmus von 100 zur Basis 10 gleich 2 ist:
log_10(100) = 2
10^2 = 100Das bedeutet, die Basis ist 10 und der Exponent ist 2, sodass wir 100 erhalten.
Basiswechselregel
Die Basiswechselregel besagt, dass der Logarithmus einer Zahl zur Basis b1 gleich dem Logarithmus der Zahl zur Basis b2 dividiert durch den Logarithmus von b1 zur Basis b2 ist. Anders ausgedrückt, der Logarithmus einer Zahl in einer Basis kann in eine andere Basis umgewandelt werden.
Formel für die Basiswechselregel:
log_b1(x) = log_b2(x) / log_b2(b1)Beispiel: Der Logarithmus von 100 zur Basis 10 in eine Basis 2 umwandeln möchten:
log_2(100) = log_10(100) / log_10(2)
log_2(100) = 2 / 0.301
log_2(100) = 6.643Das bedeutet, der Logarithmus von 100 zur Basis 2 ist ungefähr 6.643.
Die Rechenregeln für Logarithmen sind wichtig, um komplexe Berechnungen durchzuführen. Die Multiplikationsregel, Divisionsregel, Potenzregel, Umkehrregel und Basiswechselregel ermöglichen es, komplexe Berechnungen durchzuführen und Logarithmen in verschiedenen Basen umzuwandeln. Es ist wichtig, diese Rechenregeln zu verstehen und anzuwenden, um ein besseres Verständnis für Logarithmen zu entwickeln und sie in verschiedenen Anwendungen erfolgreich anzuwenden.
Anwendungsbereiche von Logarithmus

Logarithmen finden in vielen Bereichen der Mathematik, Wissenschaft und Technik Anwendung. In der Geometrie werden sie zum Beispiel zur Berechnung von Flächen- und Volumenelementen verwendet. In der Physik werden sie verwendet, um die Schallintensität, den pH-Wert von Lösungen oder das Wachstum von Populationen zu beschreiben. In der Informatik sind Logarithmen ein wichtiger Bestandteil von Datenstrukturen und Algorithmen, insbesondere bei der Analyse der Laufzeit von Algorithmen. Weitere Anwendungen von Logarithmen sind:
- Finanzmathematik
- Statistik
- Algorithmen
- Modellierung von Wachstumsraten
- Regressionsanalysen
- Ingenieurwesen
- Naturwissenschaften
Tipp: Insbesondere in der Finanzmathematik spielen Logarithmen eine wichtige Rolle, zum Beispiel bei der Berechnung von Zinseszinsen oder der Bewertung von Aktien und Anleihen.
Entdecke hier hervorragende Einführungen in Algorithmen:
Praktische Tipps zur Anwendung von Logarithmen
Wenn Du mit Logarithmen arbeitest und Logarithmus anwenden möchtest, gibt es ein paar wichtige Dinge zu beachten. Einige der wichtigsten Tipps zum Berechnen von Logarithmen werden Dir im Folgenden vorgestellt.
- Kenne die Regeln: Die Regeln für die Berechnung von Logarithmen sind entscheidend, um komplexe Berechnungen durchzuführen. Es ist wichtig, die Regeln für die Multiplikation, Division und Potenzierung von Logarithmen zu kennen.
- Wandle um: Logarithmen können komplexe Berechnungen vereinfachen, indem sie die Multiplikation von Zahlen in Additionen umwandeln. Nutze diese Eigenschaft, um Berechnungen zu vereinfachen.
- Achte auf die Basis: Logarithmen werden in Bezug auf eine bestimmte Basis ausgedrückt, die normalerweise eine Zahl zwischen 2 und 10 ist. Es ist wichtig, die Basis zu kennen und zu berücksichtigen, wenn Du mit Logarithmen arbeitest.
- Beachte die Definitionsmenge: Logarithmen sind nur für positive Argumente definiert. Wenn Du mit negativen Zahlen oder Null arbeitest, musst Du andere Methoden verwenden.
- Verstehe die Bedeutung: Logarithmen haben eine klare Bedeutung und können z.B. zur Bestimmung von Potenzen oder zur Umwandlung von Multiplikationen in Additionen verwendet werden. Verstehe die Bedeutung, um komplexe Berechnungen besser durchzuführen.
- Übung macht den Meister: Wie bei jeder mathematischen Funktion ist Übung der Schlüssel zur Beherrschung von Logarithmen. Nutze Übungsaufgaben, um Deine Fähigkeiten zu verbessern.
- Vermeide Fehler: Da Logarithmen kompliziert sein können, ist es wichtig, sorgfältig zu arbeiten, um Fehler zu vermeiden. Prüfe Deine Berechnungen sorgfältig und nutze einen Taschenrechner oder Computer, um sicherzugehen, dass Du korrekte Ergebnisse erhältst.
- Nutze Online-Ressourcen: Es gibt viele Online-Ressourcen, die Dir bei der Arbeit mit Logarithmen helfen können. Nutze sie, um Dein Verständnis zu vertiefen und Deine Fähigkeiten zu verbessern.
Nun solltest Du keine Probleme mehr haben, den Logarithmus richtig anzuwenden!
Ln subtrahieren – Ein Sonderfall?
Das Subtrahieren von ln – auch natürliche Logarithmen genannt – folgt den gleichen Schritten wie das Subtrahieren von ln mit anderen Basen. Wie auch bei anderen Rechnungen ist es beim Subtrahieren von ln wichtig, die Logarithmus Regeln richtig anzuwenden.
Der natürliche Logarithmus des Produktes von zwei Zahlen ist gleich der Summe der natürlichen Logarithmen der einzelnen Zahlen. Der natürliche Logarithmus des Quotienten von zwei Zahlen ist gleich der Differenz der natürlichen Logarithmen der einzelnen Zahlen.
Logarithmus Regel
Beispiel:
ln(100) - ln(10)
ln(100/10)
ln(10) = 2.3026
Daher ist ln(100) - ln(10) gleich 2.3026.
Entdecke hier gute Logarithmus Bücher:
Logarithmus Regeln zusammengefasst
Logarithmen sind eine wichtige mathematische Funktion, die in vielen Bereichen Anwendung findet. Sie ermöglichen es, komplexe Berechnungen zu vereinfachen, indem sie die Multiplikation von Zahlen in Additionen umwandeln. Mit genug Übung und Geduld kannst Du Deine Fähigkeiten verbessern und ein Experte im Umgang mit Logarithmen werden!
FAQ – Alles Wichtige über Logarithmus Regeln auf einem Blick
Nein, man kann keine Zahlen direkt mit dem Logarithmus multiplizieren. Der Logarithmus ist eine mathematische Funktion, die zur Lösung von Potenzgleichungen verwendet wird.
Du kannst in einen Logarithmus keine negativen Zahlen oder 0 einbeziehen, da Logarithmen nur mathematische Gleichungen und Zahlen größer als 0 lösen können.
Der Logarithmus wird in mathematischen und wissenschaftlichen Anwendungen genutzt, um Probleme zu lösen, in denen eine exponentielle oder logarithmische Funktion beteiligt ist. Zum Beispiel wird der Logarithmus in elektronischen Projekten und bei der Entwicklung von Apps verwendet.



