Das Wichtigste in Kürze
Sollten Zähler und Nenner eines Bruches denselben Teiler haben, können sie gekürzt werden, wie Du anhand dieser Beispiele siehst.
Um auf die einfachste Form des jeweiligen Bruches innerhalb der Bruchrechnung zu kommen, kürzt man sie. Hier mehr zu den Einsatzgebieten der Bruchrechnung.
Zwecks der Multiplikation und des Dividierens ist das Kürzen über Kreuz möglich. Für das Addieren und Subtrahieren gelten andere Regeln. Hier mehr zu Hilfsmitteln im Unterricht.
Brüche zu kürzen, kann anfangs wie ein Puzzle wirken. Dieser Blogbeitrag erklärt Dir grundlegende Dinge: Was Bruchrechnung ist, nach welchen Regeln Du beispielhaft welche Brüche wie kürzen kannst und wo die Bruchrechnung zum Einsatz kommt. Weiterhin geben wir einen Exkurs zum Thema Hilfsmittel im Matheunterricht.
Inhalt
Bruchrechnung: Was ist das?
Bruchrechnung ist ein Teilgebiet der Mathematik, das sich mit Brüchen beschäftigt.
Ein Bruch ist eine Darstellung von Teilen eines Ganzen, zum Beispiel als Anteil oder Verhältnis. Brüche bestehen aus zwei Teilen: dem Zähler und dem Nenner.
- Der Zähler gibt an, wie viele Teile von etwas vorhanden sind.
- Während gibt der Nenner an, in wie viele Teile das Ganze geteilt wurde.
Die Rechenregeln der Bruchrechnung umfassen das Addieren, Subtrahieren, Multiplizieren und Dividieren von Brüchen.
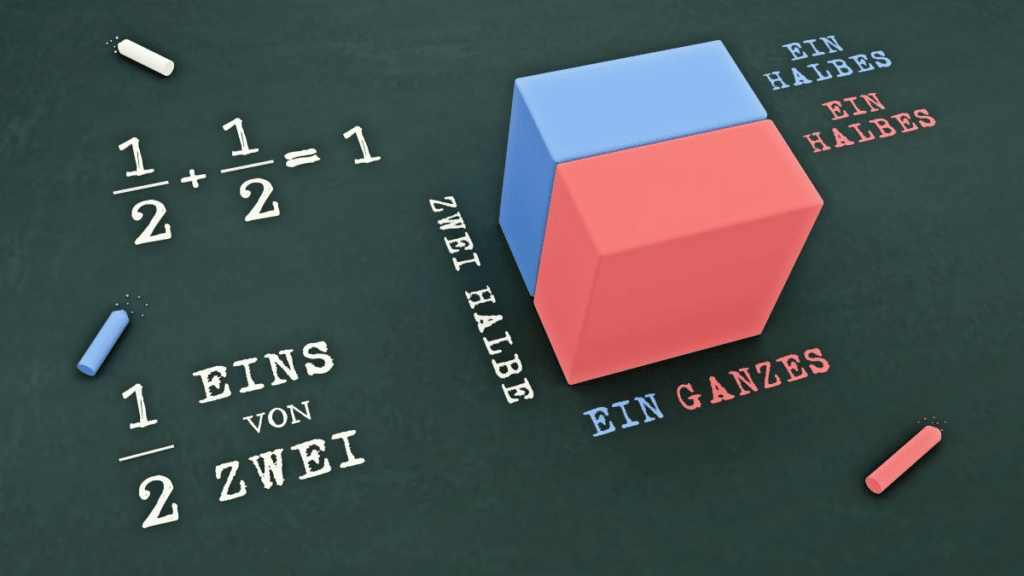
Warum muss man Brüche kürzen?
Man muss Brüche kürzen, um sie in eine einfache Form zu bringen. Ein Bruch ist in seiner einfachsten Form, wenn Zähler und Nenner keinen gemeinsamen Teiler mehr haben. Das bedeutet, dass der Bruch nicht weiter gekürzt werden kann. Es gilt also: Kürze so weit wie möglich.
Das Kürzen ist besonders nützlich, wenn man Brüche addieren, subtrahieren, multiplizieren oder dividieren möchte, da es das Rechnen mit ihnen einfacher macht.
- Um Brüche addieren oder subtrahieren zu können, müssen sie denselben Nenner haben. Wenn sie das nicht tun, müssen sie zuerst auf den kleinsten gemeinsamen Nenner gebracht werden.
- Damit man Brüche multiplizieren kann, werden die Zähler und Nenner miteinander multipliziert.
- Um Brüche zu dividieren, wird der erste Bruch mit dem Kehrwert des zweiten Bruchs multipliziert.
Hinweis: Brüche können auch in Dezimalzahlen umgewandelt werden, indem der Zähler durch den Nenner dividiert wird. Es ist wichtig zu beachten, dass einige Brüche periodische Dezimalzahlen ergeben können, die eine unendliche Anzahl von Ziffern haben.
Beispiele: Brüche kürzen
Wann darf ich bei einem Bruch kürzen?
Ein Bruch kann gekürzt werden, wenn Zähler und Nenner einen gemeinsamen Teiler haben. Das bedeutet, dass man beide durch den gleichen Faktor teilen kann, um den Bruch zu vereinfachen. Vergiss nicht: Kürze so weit wie möglich.
Bevor man jedoch kürzt, sollte man immer prüfen, ob der gekürzte Bruch auch noch den gleichen Wert wie der ursprüngliche Bruch hat. Wenn der gekürzte Bruch nicht mehr den gleichen Wert hat, darf man nicht kürzen.
Beispiel 1: Brüche mit einem gemeinsamen Teiler
Gegeben ist der Bruch 6/12.
Um diesen Bruch zu kürzen, sucht man zuerst den größten gemeinsamen Teiler von Zähler und Nenner. In diesem Fall ist der größte gemeinsame Teiler 6.
Zähler und Nenner werden durch 6 geteilt, um den Bruch zu kürzen:
6/12 = (6 ÷ 6) / (12 ÷ 6) = 1/2
Der gekürzte Bruch ist 1/2.
Dadurch hat man den Nenner weitern können.
Beispiel 2: Brüche mit einem ungewöhnlichen Teiler
In diesem Beispiel ist der Bruch 15/35 gegeben.
Um diesen Bruch zu kürzen, muss man ebenfalls den größten gemeinsamen Teiler von Zähler und Nenner finden. In diesem Fall ist der größte gemeinsame Teiler 5.
Zähler und Nenner werden hier durch 5 geteilt, um den Bruch zu kürzen:
15/35 = (15 ÷ 5) / (35 ÷ 5) = 3/7
Der gekürzte Bruch ist 3/7.
Beispiel 3: Brüche mit unterschiedlichen Teilern
Als drittes ist der Bruch 10/28 gegeben.
Was ist hierbei der größte gemeinsame Teiler von Zähler und Nenner? In diesem Fall ist der größte gemeinsame Teiler 2.
Zähler und Nenner werden durch 2 geteilt, um den Bruch zu kürzen:
10/28 = (10 ÷ 2) / (28 ÷ 2) = 5/14
Der gekürzte Bruch ist 5/14.
Beispiel 4: Brüche erweitern bei der Addition
Gegeben sind nun die Brüche 3/8 und 5/12.
Um diese Brüche zu addieren, müssen sie auf einen gemeinsamen Nenner gebracht werden. Der kleinste gemeinsame Nenner ist 24.
Beide Brüche werden mit den entsprechenden Faktoren erweitert: 3/8 wird mit 3/3 erweitert (3 x 3 = 9) und 5/12 wird mit 2/2 erweitert (5 x 2 = 10).
Die Brüche lauten nun 9/24 und 10/24.
Sie haben den gemeinsamen Nenner 24, so dass man sie addieren kann:
9/24 + 10/24 = 19/24
Der Bruch 19/24 kann nun gekürzt werden, indem Zähler und Nenner durch ihren größten gemeinsamen Teiler, der in diesem Fall 1 ist, geteilt werden.
Der gekürzte Bruch lautet somit 19/24.
Tipp: Solltest Du Schwierigkeiten mit dem Bruchrechnen haben, kannst Du jederzeit Deine Eltern oder Deine Lehrer um Hilfe fragen. Alternativ gibt es auch eine Vielzahl von Erklärungsvideos im Netz.
Beispiel 5: Brüche bei der Subtraktion
Im fünften Beispiel sind die Brüche 7/9 und 1/3 gegeben.
Um diese Brüche zu subtrahieren, müssen sie ebenfalls auf einen gemeinsamen Nenner gebracht werden. Der kleinste gemeinsame Nenner ist 9. 7/9 bleibt unverändert, während 1/3 mit 3/3 erweitert wird (1 x 3 = 3).
Der Bruch lautet nun 3/9.
Beide Brüche haben den gleichen Nenner 9, so dass man sie subtrahieren kann:
7/9 – 3/9 = 4/9
Der Bruch 4/9 kann nun gekürzt werden, indem man Zähler und Nenner durch ihren größten gemeinsamen Teiler, der in diesem Fall 4 ist, teilt.
Der gekürzte Bruch lautet somit 1/4.
Beispiel 6: Brüche bei der Multiplikation und Division
Zum Schluss sind die Brüche 2/5 und 6/7 gegeben.
Um diese Brüche zu erweitern bzw. multiplizieren, multipliziert man Zähler und Nenner miteinander:
2/5 x 6/7 = 12/35
Der Bruch 12/35 kann nun gekürzt werden, indem man Zähler und Nenner durch ihren größten gemeinsamen Teiler, der in diesem Fall 1 ist, teilt.
Der gekürzte Bruch lautet somit 12/35.
Um diese Brüche zu dividieren, multipliziert man den ersten Bruch mit dem Kehrwert des zweiten Bruchs:
2/5 ÷ 6/7 = 2/5 x 7/6 = 14/30
Der Bruch 14/30 kann nun gekürzt werden, indem man Zähler und Nenner durch ihren größten gemeinsamen Teiler, der in diesem Fall 2 ist, teilt.
Der gekürzte Bruch lautet somit 7/15.
Kann man Brüche über Kreuz kürzen?
Nein, man kann Brüche nicht nur über Kreuz kürzen.
Das sogenannte „Kürzen über Kreuz“ ist eine Methode, um zwei Brüche zu einem Bruch zusammenzufassen, wenn sie in einer Division stehen. Dabei wird der Zähler des ersten Bruchs mit dem Nenner des zweiten Bruchs multipliziert und umgekehrt. Das heißt, man kann den Bruch mit Zähler und Nenner erweitern.
Wenn ein Bruch allerdings alleine steht oder man mehrere Brüche addieren oder subtrahieren möchte, muss man andere Methoden anwenden, um zu kürzen.
Man kann zum Beispiel den größten gemeinsamen Teiler von Zähler und Nenner bestimmen und beide durch diesen Teiler teilen. Oder man kann den Bruch in eine Dezimalzahl umwandeln und die Dezimalstellen auf eine bestimmte Anzahl runden, um den Bruch zu vereinfachen.
Einsatzgebiete der Bruchrechnung
Bruchrechnung ist eine wichtige Fähigkeit in vielen Bereichen der Mathematik, insbesondere in der Algebra und Geometrie. Aber die Bruchrechnung ist auch ein Thema, das im Alltag nützlich ist. Es gibt viele praktische Anwendungen für Brüche im täglichen Leben.
- Kochen: Wenn Du ein Rezept kochst, musst du oft Zutaten in Bruchteilen hinzufügen. Du könntest zum Beispiel 3/4 Tasse Milch oder 1/2 Teelöffel Salz hinzufügen. Wenn Du die das Kürzen und die Bruchrechnung nicht beherrschst, könnte es schwierig sein, die richtige Menge der Zutaten zu messen und das Rezept könnte schief gehen.
- Einkaufen: Gehst Du im Supermarkt einkaufen, begegnest Du oft Brüchen. Zum Beispiel könnte eine Packung mit 2 1/2 Pfund Äpfeln im Angebot sein. Wenn du den Preis pro Pfund berechnen möchtest, musst Du die Gesamtkosten durch das Gewicht in Pfund teilen. Ohne Bruchrechnung könntest Du Schwierigkeiten haben, solche Berechnungen durchzuführen.
- Handwerk und DIY-Projekte: Bruchrechnung wird auch bei handwerklichen und DIY-Projekten benötigt. Zum Beispiel könntest Du bei der Arbeit mit Holz eine Tafel mit den Abmessungen 3/4 Zoll x 2 Zoll x 6 Fuß benötigen. Wenn Du nicht in der Lage bist, diese Maße in Brüche umzuwandeln und Berechnungen durchzuführen, könnte es schwierig sein, das Projekt erfolgreich abzuschließen.
- Finanzen: In der Finanzwelt begegnen uns auch oft Brüche. Beispielsweise kann die Verzinsung eines Bankkontos als Bruch dargestellt werden, zum Beispiel 1,5 % oder 2,25 %. Wenn Du Dein Einkommen und Deine Ausgaben in einem Haushaltsbudget verwaltest, kann Bruchrechnung nützlich sein, um die richtigen Prozentsätze oder Anteile Deiner Ausgaben zu bestimmen.
- Medizin: In der Medizin wird auch oft mit Brüchen gearbeitet. Zum Beispiel könnte ein Patient eine Dosierung von 1/2 Tablette oder 1/4 Teelöffel eines Medikaments erhalten. Die richtige Dosierung ist entscheidend für die Gesundheit des Patienten, daher ist es wichtig, dass Ärzte und Pflegekräfte mit Brüchen vertraut sind.
Exkurs: Hilfsmittel im Unterricht

Im Mathematikunterricht benötigt man einige Hilfsmittel, um die Arbeit mit Zahlen und Formeln zu erleichtern und zu unterstützen. Hier sind einige der wichtigsten Hilfsmittel, die du im Mathematikunterricht benötigen könntest:
- Taschenrechner: Ein Taschenrechner ist ein grundlegendes Hilfsmittel, das im Mathematikunterricht eingesetzt wird. Er kann die Arbeit bei der Lösung von Gleichungen und der Durchführung von Berechnungen erleichtern.
- Geodreieck: Ein Geodreieck ist ein Werkzeug, das verwendet wird, um Winkel und Linien zu messen oder zu zeichnen. Es kann nützlich sein, um geometrische Formen zu konstruieren und Messungen genau vorzunehmen.
- Lineal: Ein Lineal ist ein weiteres Werkzeug, das zum Messen von Längen und zur Konstruktion von Geraden und Formen verwendet wird. Es kann helfen, genauere Messungen durchzuführen und Formen präziser zu zeichnen.
- Formelsammlung: Eine Formelsammlung ist ein Buch oder eine Zusammenstellung von Formeln, die in der Mathematik verwendet werden. Sie kann als Referenzwerkzeug dienen und bei der Lösung von komplexeren Problemen helfen.
- Grafikrechner: Ein Grafikrechner ist ein fortschrittliches Werkzeug, das im Mathematikunterricht verwendet wird. Es kann verwendet werden, um mathematische Funktionen zu graphieren, komplexe Berechnungen durchzuführen und verschiedene Formeln und Gleichungen zu lösen.
- Schreibutensilien: Schreibutensilien wie Bleistifte, Kugelschreiber, Radiergummis und Lineale sind unverzichtbare Hilfsmittel im Mathematikunterricht. Sie helfen dabei, Aufgaben und Gleichungen sauber und ordentlich zu notieren, Fehler zu korrigieren und Prüfungsaufgaben zu lösen.
Alles Wichtige zum Thema Brüche kürzen auf einen Blick
Bruchrechnung ist eine wichtige Fähigkeit in vielen Bereichen der Mathematik, insbesondere in der Algebra und in der Geometrie. Sie wird auch in vielen Alltagssituationen angewendet, wie zum Beispiel beim Kochen, beim Einkaufen oder beim Teilen von Gegenständen unter Freunden. Man kann unterschiedliche Regeln (auch beim Erweitern von Brüchen) anwenden, darunter Addieren, Subtrahieren, Multiplizieren und Dividieren. Es gilt: Kürze so weit wie möglich.
FAQ zum Thema Brüche kürzen
Nehmen wir 6/12. Zum Kürzen muss man den größten gemeinsamen Teiler von Zähler und Nenner finden, hier: 6. Zähler und Nenner werden durch 6 geteilt: 6/12 = (6 ÷ 6) / (12 ÷ 6) = 1/2.
Um Brüche so weit wie möglich zu kürzen, muss man den größten gemeinsamen Teiler von Zähler und Nenner finden.
Wenn der größte gemeinsame Teiler 1 ist, kann der Bruch nicht weiter gekürzt werden. Wenn er größer als 1 ist, teilt man Zähler und Nenner durch diesen Teiler, bis sie nicht mehr weiter teilbar sind.